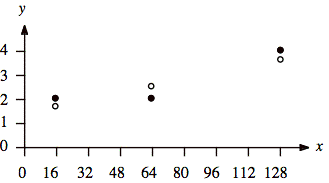
Ex:            Find a way to fit three data points, with an exponential curve:

where

        (x1, y1) = (16, 2)          (x2, y2) = (64, 2)            (x1, y1) = (128, 4)

Here, we have since is one-dimensional.

We proceed by calculating derivatives:

Next, we solve :

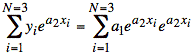
and

or

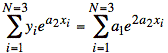
and

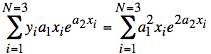
At this point, the idea is to take the coefficients, a1 and a2, outside the summations. Here, we can take a1 outside:

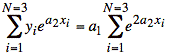
and

Our goal is to have summations involving only the data. Unfortunately, we are unable to extract a2 from the summations. Thus, this direct approach fails to yield a simple solution. We might try to use an iterative method, but this adds considerable complexity.

An alternative approach is to take logarithms of data points and the model function:

Note:       We have chosen to change the problem we are solving so we can apply the least-squares method in a straightforward way.

We set derivatives to zero:

We proceed by calculating the derivatives:

and

We can now take coefficients outside of the summations:

or

and

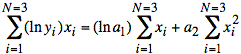
We define α1 to simplify the appearance of our equations:

        α1 ≡ ln a1

Writing the equations in matrix form, we have the following result:

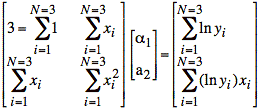
or in symbolic form:

Our solution in matrix notation is obtained by multiplying both sides by X−1:

Using the numerical data provided in the problem, we have the following calculation:

or

or

or

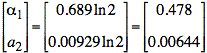
or

, a2 = 0.00644

or

For the data points, we get the following y values: