|
|
By: Neil E. Cotter |
Regression |
|
|
|
Least squares method |
|
|
|
|
|
|
|
|
|
|
|
|
Tool: A regression
fit of a chosen function form to a set of data is obtained by picking
coefficients that minimize the total squared difference (or error) between the
function and the data. (If the function form is a polynomial, for example, the
parameters are the coefficients of the polynomial.) The data points, ![]() , are located at points
, are located at points ![]() in an N‑dimensional
space. We denote the function fit as
in an N‑dimensional
space. We denote the function fit as ![]() , where
, where ![]() contains the coefficients
of f.
contains the coefficients
of f.
E ≡ SSE ≡Sum of Squared Errors of all observations

From calculus, the least squares solution is to set the derivatives of the total squared error with respect to a1, ..., aM equal to zero.
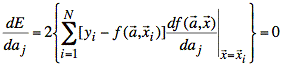
Note: The sum is over i, but the derivative is with respect to j.
Not'n: ![]()
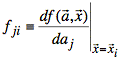
Using this notation, we find a1, ..., aM by solving the following equation:

or
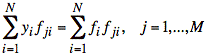
Note: We get M equations in M unknowns—one for each aj.