Ex:            Find a multiple regression (i.e., hyperplane) fit of tensile strength versus composition for the following data for the hardness of steel, (adapted from [1]):

TABLE I

Ferritic Stainless Steels

 

Sol'n:       The hyperplane is defined as follows:

There are various difficulties with the data and the vague problem statement that we wish to resolve before attempting to find the multiple regression fit. First, we observe that Mn, Si, P, and S are constant (except for the peculiar product 409). Since product 409 has one-of-a-kind composition with respect to Titanium, we ignore it. To obtain a meaningful fit, we need to either hold variables constant or have enough data to cover the possible combinations of variations of variables. Here, we will hold Mn %, Si %, P %, and S % constant, and we will model the effects of changes in C % and Cr %.

Second, we eliminate products with peculiar characteristics in the "Other" column (with the exception of product 405). Thus, we now eliminate products 434 and 446. We retain product 405 for no better reason than that we will need it in order to have enough data for the multiple regression, and intuition suggests that the small concentration of Aluminum makes little difference in the tensile strength. (Such questionable assumptions are often made when dealing with real data, and it is imperative that they be recognized, specified, and then verified. Here, we proceed without verification.)

Third, we eliminate products 436 and 444, owing to their lack of values for composition.

Fourth, we must decide how to deal with the Cr values that are given as ranges. An arbitrary decision is made to us the highest value in the range. This leaves us with only the four data points in Talbe II. The values that enter into the multiple regression are shown in bold. This means our solution is applicable only when Mn, Si, P, and S have the fixed values in the table.

TABLE II

Ferritic Stainless Steels Selected Data

The hyperplane for the regression fit is defined as follows:

We write matrix terms for the data and hyperplane fit:

                                                                           

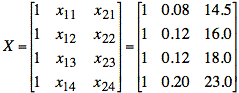
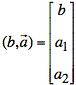
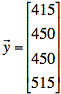
The matrix equation for the data and hyperplane fit are as follows:

A pseudoinverse of X yields the least-squares (i.e., regression) solution:

where

Not'n:      XT ≡ X transpose

Using Matlab™, we obtain the following result:

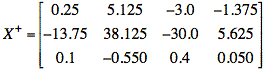
and

Plugging the (x1, x2) coordinates into the hyper-plane equation yields the following estimated y values:

or

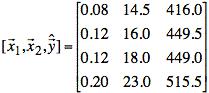
The errors are found by subtracting estimated y values from actual y values:

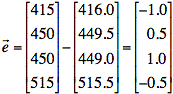
In the plot below, the estimates are shown as circles:

Note:       In this problem, we might do just as well by using linear interpolation with the x coordinates on a line connecting the first and last points and collapsing the middle two points into a single point with y = 450.

Note:       More data would yield a more credible fit. With so few data points, extrapolating from the above fit would be hazardous.

Ref:    [1] Vladimir B. Ginzburg, Steel-Rolling Technology, Theory and Practice, New York, NY: Marcel Dekker, 1989, (Tables 3.13 and 3.15).