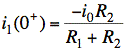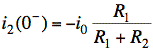|
|
By: Carl H. Durney and Neil E. Cotter |
State-space method |
|
|
|
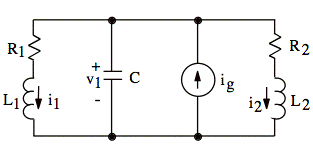
Circuits |
|
|
|
Initial conditions |
|
|
|
Example 2 |
|
|
|
|
|
|
By: Carl H. Durney and Neil E. Cotter |
State-space method |
|
|
|
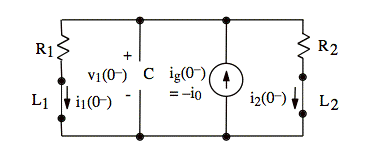
Circuits |
|
|
|
Initial conditions |
|
|
|
Example 2 |
|
|
|
|