Tool:       One-way Analysis of Variance (ANOVA) tests the hypothesis that means are all the same for various treatments applied to a system, [1, 2].

Assumptions:

        1)    There are k different treatments (samples) under consideration

        2)    For the ith of k different treatments (samples), there are ni observations

        3)    All of the k treatments (samples) have the same variance, σ

        4)    The null and alternate hypotheses relate to equal means:

                H0: μ1 = μ2 = ... = μk

                H1: At least one of the means is not equal to the others

Definitions:

        α    ≡   significance level for rejecting null hypothesis

        k     ≡   total number of samples (treatments) being considered

        i      ≡   index designating which sample (treatment) is being considered

        N    ≡   total number of observations (data points) available for all treatments

        ni    ≡   number of observations available for sample (treatment) i

        n     ≡   number of observations available for each sample if all ni are equal

            ≡   index designating which of ni observations of sample i is being considered

            ≡   grand mean of all observations for all samples

           ≡   actual mean value for ith treatment

          ≡   difference between actual mean and grand mean for sample i: αi = μi − μ

          ≡   difference between jth observation of ith sample and μi: εij = xij − μi

          ≡   value of observation i for sample (treatment) j: xij = μ + αi + εij

          ≡   calculated mean for all observations from ith sample (treatment)

          ≡   calculated mean for all observations from all samples

        SSA ≡ Sum of Squared errors of All treatment (sample) means vs grand mean

        SSE ≡ Sum of Squared Errors of all observations vs respective sample means

        SST ≡ Sum of Squared errors Total for all observations vs grand mean = SSA + SSE

       MSA ≡ calculated Mean of Sum of All treatment squared errors;

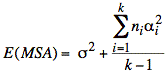
       MSE ≡ calculated Mean of Sum of squared Errors;

ANOVA calculations:

       

       

       

       

       

       

       

       

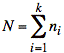
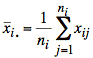
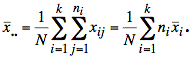
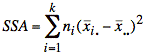
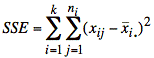
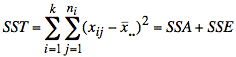
        if H0 is true

        H0 rejected if f exceeds F-distribution critical value fa(ν1=k−1,ν2=N−k)

Theory:   From the definition of the αi, the null and alternate hypotheses, H0 and H1, are equivalent to the following statements:

H0: α1 = α2 = ... = αk

H1: At least one αi ≠ 0

The MSA and MSE give different estimates of the variance:

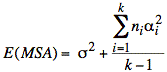with k − 1 degrees of freedom

and

with N − k degrees of freedom

If the null hypothesis is true, the extra term in the MSA estimate is zero since all the αi are zero. In that case, the ratio of MSA to MSE will have an F-distribution with k − 1 and N − k degrees of freedom. We may then use the critical value of the F-distribution from a table to determine if the ratio of MSA to MSE is in the range expected if all the αi are zero. If the ratio exceeds the critical value, then we may assume that the second term in E(MSA) was not zero after all, and we reject the null hypothesis.

Note:       Since an F-distribution describes ratios of variances, and variances are always positive, an F-distribution is nonzero only for positive values of f. Thus, critical values of the F-distribution are always positive numbers, and we use a one-sided confidence interval or one-sided hypothesis test in the ANOVA method.

Note:       The ANOVA method assumes σ is the same for all observations. This might be true, for example, if errors only arise from measurement techniques that are the same for all samples. Bartlett's test is a useful tool for determining if the variances are equal.

Note:       If we use the same number of observations for all samples (treatments), then the f-ratio is relatively insensitive to small differences in variances, [1].

Ref:    [1] Ronald E. Walpole, Raymond H. Myers, Sharon L. Myers, and Keying Ye, Probability and Statistics for Engineers and Scientists, 8th Ed., Upper Saddle River, NJ: Prentice Hall, 2007.

            [2] Anthony J. Hayter, Probability and Statistics for Engineers and Scientists, 2th Ed., Pacific Grove, CA: Duxbury, 2002.