Thm:         Given n Bernoulli trials with probability of success for each trial being p, the probability, P(m of n), of exactly m successes in n trials approaches the probability density of x = m for a normal (i.e., gaussian) distribution with μ = np and σ2 = npq:

.

Proof:     We follow the general method of proof given in [1].

For Bernoulli trials we have the following value for P(m of n):

where is the combinatoric coefficient.

For the proof, we consider different values of n, and we will consider m to be a fixed number, k, of standard deviations from the mean as n increases.

Note:       Although m is an integer, the method of proof allows k to have any real value.

We use Stirling's formula, [2], to approximate the factorials in nCm:

where n > 0 and 0 < θ < 1.

Note:       Stirling's formula is related to the Stirling series expansion of the gamma function in powers of 1/n, (see [3]). The Stirling series has the curious property that it produces very accurate approximations of the gamma functions with only a few terms—and actually diverges if all the terms are used.

Using Stirling's formula for the terms of nCm, yields the following expression:

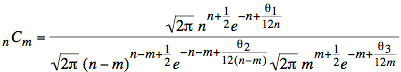
As n becomes large, so do n − m and m, and the residual terms involving θ1, θ2, and θ3 become vanishingly small. Thus, we may eliminate the θ terms and, after also canceling common factors of and the exponentials of e, write the following expression:

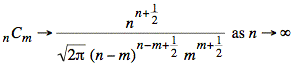
If we split the nn term into two pieces in the numerator, we can match up the exponents in the numerator and denominator:

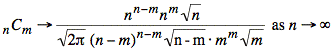
or

Now we invert the terms being exponentiated and use the following formulas:

and

Substituting these expressions yields the following equation:

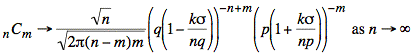
The terms having n in their denominators will become small as n becomes large. Thus, we use an approximation that exploits this behavior:

for x small

or

for x small (from Taylor series for ln)

Applying this identity to our formula for the combinatoric coefficient, we have the following expression:

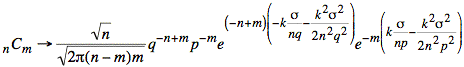
Using m = np + ks and m − n = −nq + ks we have

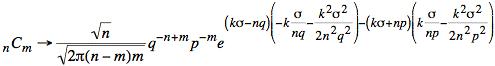
If we consider just the exponent, we have the following calculation:

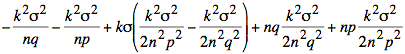
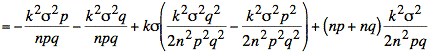
Using s2 = npq the simplification of the exponent continues:

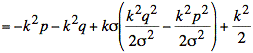
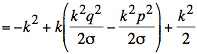
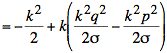
We observe that the second term is proportional to and vanishes as n becomes large. Dropping this term yields the following expression:

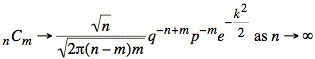
If we now multiply by the probability, of one particular pattern of m successes occurring, we obtain the following expression:

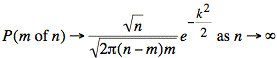
We have the following simplification for the factor in front:

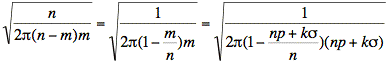
For n large, ks is much smaller than n, leading to the following result:

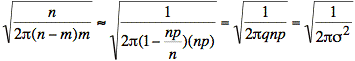
With this substitution, and using we complete our proof:

Ref:    [1] Eugene Lukacs, Probability and Mathematical Statistics, an Introduction, New York, NY: Academic Press, 1972.

            [2] Milton Abramowitz and Irene A. Stegun, Eds., Handbook of Mathematical Functions: National Bureau of Standards Applied Mathematics Series 55, Washington, D.C.: Government Printing Office, 1972.

            [3] Carl M. Bender and Steven A. Orszag, Advanced Mathematical Methods for Scientists and Engineers, New York, NY: McGraw-Hill, 1978.