Tool:       The sample variance, S2, is an unbiased estimate of variance σ2, (when the samples, Xi, are independent and identically distributed). (This accounts for why the formula employs a multiplicative factor of instead of .)

Deriv:      S2 is an unbiased estimate of variance σ2 means E(S2) = σ2.

We use tools for linear combinations of random variables from probability to compute E(S2), starting from the definition of S2.

By symmetry and independence of the Xi, we can argue that each term of the summation must have the same expected value as the first term:

If we expand the sample mean, we have the following:

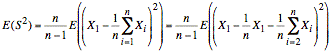
or

The above expression reveals that using X1 in the sample mean as well as in the distance from the sample mean reduces the effective value of X1 by a factor of (n − 1)/n. The remainder of the derivation consists of manipulations that ultimately demonstrate that the estimated sample variance we would obtain by taking the average of squared distances of samples from the sample mean is reduced by this same factor. In other words, using the data to compute a sample mean results in a mean that is closer to the sample values than it should be. It is closer by a factor of (n − 1)/n.

We now expand the term in the expected value.

or

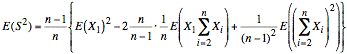
Note:       The summations in the above equation start at i = 2, and the factor in front has been inverted.

Exploiting the independence of the Xi, we have the following identity for the middle term:

For the third term, we have the following expansion:

Again exploiting the independence and identical distributions of the Xi, we have the following:

In the expected value, we get an term plus n − 2 terms of the form E(Xi)E(Xj≠i) that yield a value of μ2:

Making substitutions based on these identities, we have the following:

Since all Xi are identically distributed, we may use a generic X in place of X1 or X2:

or

or

or

or

Thus, S2 is verified to be an unbiased estimate of the variance, σ2.