Ex:           An engineer measures the following beta values for bipolar transistors with the aim of finding nominal values of gain, (i.e., beta), to list on a datasheet. The sample variance is also of interest, as it serves as a guide to min and max values to list on the datasheet.

        β1 = 111      β2 = 136      β3 = 159      β4 = 141      β5 = 109      β6 = 121

        β7 = 117      β8 = 105      β9 = 99        β10 = 102

Find the sample variance and sample standard deviation of the data.

Sol'n:      The sample variance, S2, is almost the average of the squared differences between data values and the sample mean, (which is the average data value):

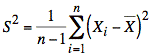where n ≡ number of data values

Notice, however, that the sum of the squared differences is divided by n − 1 rather than n. The reason for this curious feature of the sample variance is that it makes S2 an unbiased estimator. That is to say, the expected value of S2 equals the true variance of the data.

Although we forego the detailed proof here, the proof that n − 1 gives an unbiased estimator begins with a substitution of for . After squaring and canceling cross terms, we find that the first term in parentheses has a variance of σ2 and the second term in parentheses has a variance of σ2/n. Thus, the second term is responsible for the −1 in the n − 1. What has happened is that we have used our data twice when we use in place of μ. This overuse of the data increases the variance of S2.

Using a spreadsheet to compute the sample mean of the data, we find the following:

Calculation of S2 gives the following value:

The sample standard deviation is S = .

S ≈ 14.5