Tool:      The random variable T, defined as follows, is the sampled data analogue of a standard normal (or gaussian) distribution. Because the value of T depends on S, however, T has a t-distribution that differs slightly from the standard normal (or gaussian) distribution.

where

n ≡ number of data points, Xi, (which are independent and normally distributed with mean μ and variance σ)

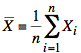≡ sample mean

≡ sample variance

The probability density function of T is a t-distribution with ν = n − 1 degrees of freedom:

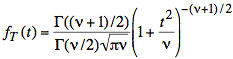
Deriv:     The first step is to express T in terms of random variables with known distributions:

where

             and               

As shown in other Conceptual Tools, Z has a standard normal (or gaussian) distribution, and χ2 has a chi-squared distribution with ν = n − 1 degrees of freedom:

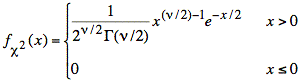
As shown in another tool, Z and χ2 are also independent. This allows us to write the joint distribution of Z and χ2 as the product of the respective probability density functions for Z and χ2:

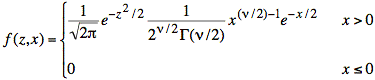
To find the probability density for T, we consider the cumulative distribution for T and take its derivative:

Note:      We treat the case of t > 0. We have t in the lower limit in this case because larger values of x give smaller values of t. For the case of t < 0, we would integrate from −∞ to t.

We move the derivative inside the outer integral and write the lower limit in terms of the x more clearly:

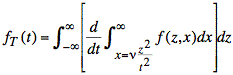
The chain rule yields an interpretation of the derivative of the integral:

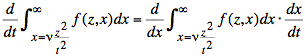
or

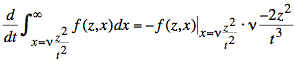
Making this substitution, we have the following expression:

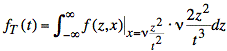
Now we use the expression for f(z, x), assuming t > 0:

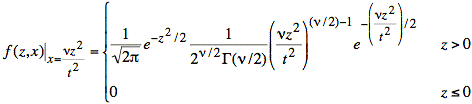
Note:      We have the condition that z > 0 because the definition of T requires Z > 0 to achieve T > 0. (X and are always positive.)

Incorporating the constraint on z into the lower limit of the outer integral yields the following expression:

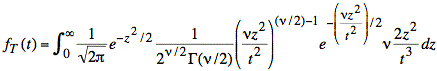
It is helpful to define a term for the constants:

Using this new term, we have the following expression:

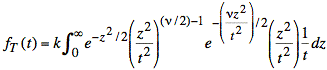
or

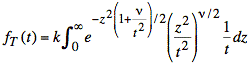
We define the following variable that allows us to use a convenient change of variables:

We have the following relationships for the change of variables:

, ,

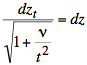and

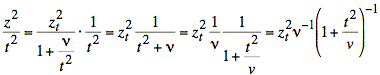
In terms of zt we have the following integral expression:

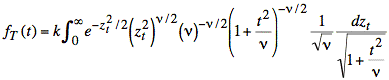
or

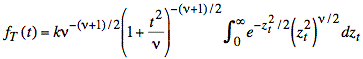
We change variables again in order to make the integrand have the form of a chi-squared distribution:

We have the following relationships for the change of variables:

, ,

In terms of w we have the following integral expression:

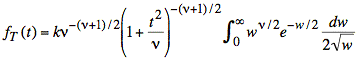
By moving appropriate constants inside the integral, we obtain the integral of an entire chi-squared distribution with ν + 1 degrees of freedom. In other words the probability represented by the following integral must equal unity:

It follows that we have the following expression for the probability density function for T:

Simplification of the constants yields the final result: