Tool:      For samples from a normal (or gaussian) distribution with mean μ and variance σ2, the distribution of the sample mean, , for n samples is normal (or gaussian) with the following mean and variance:

       and       

It follows that random variable Z defined as follows has a standard normal (or gaussian) distribution:

Proof:    The sample mean is the average of n independent samples.

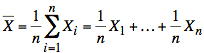
Since the sample mean is a linear combination of independent samples, it follows that the mean value of is the linear combination of the mean values of the Xi.

Since the sample mean is a linear combination of independent samples, it also follows that the variance of the sample mean is a sum of variances of the Xi each multiplied by the square of their coefficient.

Finally, we note that a linear combination of independent normal (or gaussian) random variables is a normal (or gaussian) random variable.