|
|
By: Neil E. Cotter |
Triangulation |
|
|
|
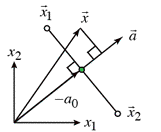
Triangle containing point |
|
|
|
Decision boundaries |
|
|
|
|
|
|
|
|
Tool: The following
procedure defines decision boundaries that may be used to determine whether a
point lies in a triangle. The rationale is that a given point, ![]() , is on the inside of the
triangle if and only if
, is on the inside of the
triangle if and only if ![]() is on the correct side of each edge of the triangle. A vector,
is on the correct side of each edge of the triangle. A vector, ![]() , is found for each side
of the triangle such that the dot product of
, is found for each side
of the triangle such that the dot product of ![]() and
and ![]() is greater than a know
constant if and only if
is greater than a know
constant if and only if ![]() is on the correct side of a particular edge of the triangle. If dot products
are large enough for all sides of the triangle, then
is on the correct side of a particular edge of the triangle. If dot products
are large enough for all sides of the triangle, then ![]() is inside the triangle.
The mathematics of defining the vector
is inside the triangle.
The mathematics of defining the vector ![]() is equivalent to
creating a decision boundary for a perceptron where the decision boundary
corresponds to an edge of the triangle. Thus,
is equivalent to
creating a decision boundary for a perceptron where the decision boundary
corresponds to an edge of the triangle. Thus, ![]() is referred to as a
decision-boundary vector. The mathematical details of the procedure for
finding
is referred to as a
decision-boundary vector. The mathematical details of the procedure for
finding ![]() follow. A 2-dimensional case is described, but the process generalizes to N
dimensions in an obvious way.
follow. A 2-dimensional case is described, but the process generalizes to N
dimensions in an obvious way.
i) Given
two points, ![]() and
and ![]() , (or N points in N dimensions), defining an edge of a triangle, the decision boundary
vector,
, (or N points in N dimensions), defining an edge of a triangle, the decision boundary
vector, ![]() , is
perpendicular to the line segment from
, is
perpendicular to the line segment from ![]() to
to ![]() . (In N‑dimensions, the decision boundary vector,
. (In N‑dimensions, the decision boundary vector, ![]() , is perpendicular to a
hyper-plane containing vertices of one side, meaning all but one vertex, of the
N‑dimensional tetrahedron.)
It follows that which side of the edge a point
, is perpendicular to a
hyper-plane containing vertices of one side, meaning all but one vertex, of the
N‑dimensional tetrahedron.)
It follows that which side of the edge a point ![]() lies on may be found by
computing the dot product of
lies on may be found by
computing the dot product of ![]() with
with ![]() and comparing it to an
appropriate constant value,
and comparing it to an
appropriate constant value, ![]() .
In particular, the dot product of
.
In particular, the dot product of ![]() and
and ![]() with
with ![]() should give the same
value,
should give the same
value, ![]() .
(These calculations correspond to projecting
.
(These calculations correspond to projecting ![]() ,
, ![]() , and
, and ![]() onto
onto ![]() .)
.)
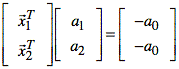
ii) These calculations may be rearranged to create a matrix equation. The equations, however is underdetermined.
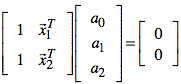
iii) To
create a solvable system of equations, a third row is needed in the matrix. In
addition, the right side is zero. This means that the augmented ![]() , which is denoted as
, which is denoted as ![]() , is unique only to
within a scaling constant. Consequently, a third-row equation may be created
by adding a third vector whose dot product with
, is unique only to
within a scaling constant. Consequently, a third-row equation may be created
by adding a third vector whose dot product with ![]() equals an arbitrary
nonzero value. This eliminates both the problem of a zero right side and a
non-unique solution. The vector forming the third row of the matrix, however,
must be linearly independent of the other two vectors. To find such a vector,
a cross product may be used. The cross product, which produces a vector,
equals an arbitrary
nonzero value. This eliminates both the problem of a zero right side and a
non-unique solution. The vector forming the third row of the matrix, however,
must be linearly independent of the other two vectors. To find such a vector,
a cross product may be used. The cross product, which produces a vector, ![]() , that is perpendicular
(normal) to the vectors in the cross product is computed as the determinant of
a matrix [1]:
, that is perpendicular
(normal) to the vectors in the cross product is computed as the determinant of
a matrix [1]:
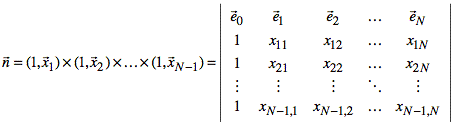
where ![]() ≡ unit vector in direction of ith axis
≡ unit vector in direction of ith axis
iv) The cross product
is added to the matrix to create a solvable system of equations that yields a
decision-boundary vector, ![]() .
.

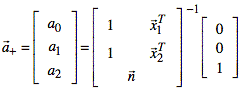
v) The final step
of the procedure is to determine whether ![]() gives a positive result
for points on the inside of the triangle under consideration. This result is
determined by computing the dot product
gives a positive result
for points on the inside of the triangle under consideration. This result is
determined by computing the dot product ![]() where
where ![]() is the unused vertex,
(which must lie on the side of the edge toward the inside of the triangle). If
s < 0, then
is the unused vertex,
(which must lie on the side of the edge toward the inside of the triangle). If
s < 0, then ![]() is replaced with
is replaced with ![]() . The calculation of
. The calculation of ![]() now indicates
now indicates ![]() is on the inside of the
edge when s > 0.
is on the inside of the
edge when s > 0.
Ref: [1] Helmut K. Fishbeck and Kurt H. Fishbeck, Formula,s Facts and Constants, 2nd Ed., Berlin, GDR: Springer-Verlag, 1987.