Tool:       The following algorithm finds the center point of an N-dimensional sphere given N + 1 points, , and is based on the idea that the center of a sphere lies on bisectors of line segments connecting points on the perimeter:

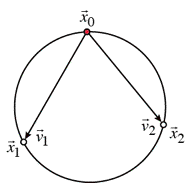
    i)  Determine vectors, , pointing from one point, , chosen as an anchor point, toward each other point.

           

   ii)  By dividing by their lengths, normalize the vectors to create unit-length vectors, , pointing from toward each other point.

               

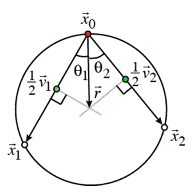
  iii)  Find the vector, , whose projection on each unit-length vector, , has its endpoint at the midpoint of the line segment from to , (i.e. the projection of on equals ). The projection of on is given by the dot product of and .

Group these equations to yield a matrix formula for .

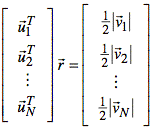
Since the vectors arise from points on a sphere, they are not dependent. Thus, the matrix equation is nonsingular and always solvable.

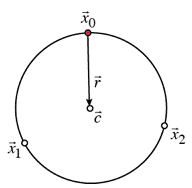
  iv)  The center point, , of the circle is found by summing and .