CONCEPTUAL TOOLS |
By: Neil E. Cotter |
Outreach |
|
|
|
Algebra Public Key |
|
|
|
Teacher's Guide |
|
|
|
|
|
|
|
|
Concept: The Public Key outreach exercise vaguely mimics public key encryption systems. In these systems, information is encoded using a public key and is decoded using a private key. The sender performs a mathematical operation with the public key to encrypt the data they are sending, and the receiver performs a mathematical operation with the private key to recover the data. Someone trying to break the code has the encoded information but not the private key.
Here, the public key, p, is a single number between 1 and 20. The data being sent, d1 and d2, are two numbers between –9 and +9. The encoding process creates a polynomial as follows:
![]() (1)
(1)
or
![]() (2)
(2)
What is sent over the internet is a data packet containing the coefficients of this cubic polynomial:
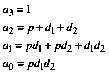 (3)
(3)
For example, if we want to send d1 = 4 and d2 = 6 with a public key of p = 3, the coefficients sent over the internet would be the following:
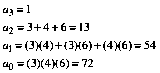 (4)
(4)
The polynomial this represents is
![]() . (5)
. (5)
The receiver possesses a private key (actually this is a process rather than a number here, whereas in the real encryption problem it would be a number) that is the formula for factoring cubic polynomials. There is a formula for this, which we are pretending only the receiver knows. Students who are curious may want to look up the formula on the web, e.g., http://www.sosmath.com/algebra/factor/fac11/fac11.html
The students' task is to try to decrypt the message without knowing the cubic equation solution. Fortunately, this is achievable with only modest effort, (unlike real codes that would simply take too long to break).
What the student has to do is factor the polynomial. One root term, x + p, is known. After this term is factored out of the cubic polynomial, what remains is a quadratic equation. For our example, the process of factoring proceeds as follows (for p = 3):
![]() (6)
(6)
or
![]() where a = 1 (7)
where a = 1 (7)
Starting with the constant term in f(x), we must have pc = 3c = 72, or c = 72/3 = 24. In general, we can find c as follows:
![]() (8)
(8)
To find b, we look at the last equation for f(x) above:
![]() (9)
(9)
From the coefficient of the squared term, we have a simple formula for b:
![]() (10)
(10)
The student can crack the code by factoring the following polynomial:
![]() (11)
(11)
Any method may be used to factor the quadratic polynomial, although the quadratic formula is an obvious choice.
![]() and
and ![]() (12)
(12)
Note that the values of d1 and d2 are the negatives of the roots. For the numbers the students will use, d1 is nonzero between –9 and 9, and d2 will always be positive from 1 to 9.
The reward students receive for finding d1 and d2 is the largest of d1 and d2, which may be paid in points or actual cash!
Set-up: The teacher has a spreadsheet listing coefficients of cubic polynomials with two integer-valued roots chosen at random. The third, integer-valued root of the cubic is positive value p that is the public key (i.e., shown to the students).
The teacher's spreadsheet also lists the roots, d1 and d2, and the value of max(d1 ,d2). The sheet has a column for entering the number of the team that is attempting to solve a given polynomial code, and the sheet has a second column for entering a 1 if the team successfully cracks the polynomial code (i.e., finds the two roots). The teacher's spreadsheet automatically calculates total payouts to each team and payouts per member.
Process: Perform the Poly Coin outreach exercise using the following steps.
I. Divide the students into teams of two, three, or four. If some teams must be smaller than other teams, they will have the advantage of having fewer team members to divide the winnings amongst. Larger teams will have the advantage of having more team members to find roots.
II. Present the idea of the code-cracking process. Students will likely find it difficult to follow the entire description of the encoding and decoding process, but students may told directly to use (8), (10), and (11). They should be able to factor the quadratic equation. Note that the students may get the negative of d1 and d2 if they use the quadratic formula, but this may be disregarded or gently corrected.
III. Have the student teams get used to the factoring process by using a practice problem:
|
x3 Coefficient |
a2 Coefficient |
a1 Coefficient |
a0 Coefficient |
p = public root |
|
a3 |
a2 |
a1 |
a0 |
p |
|
1 |
3 |
–13 |
–15 |
5 |
Solution: ![]() , payoff is
, payoff is ![]()
No money will be awarded for the example, but the values of the roots found will indicate what the factoring would have been worth.
Students should use calculators only for multiplication and addition.
The teacher and the teams should keep track of the teams assigned and the roots found. The teacher's sheet shows amounts earned and the root values. When a team finds roots, they tell the teacher, and the teacher tells them whether the roots are correct.
When a team solves a polynomial, they are allowed to pick another polynomial from the list to solve. If they get incorrect roots, that polynomial may be set aside. Team number zero may be used to indicate a failed solution.
III. Hand out the real process sheet. (Note that polynomials with smaller roots are worth less than polynomials with larger roots, but they are easier to solve. Thus, the differences in the values of polynomials are compensated for by the difficulty of solving them.) Have students call out the number of the problem their team wishes to solve. Record the team number on the spreadsheet.
When all the polynomials are used up or time is short, winnings of each team are totaled, and amounts are divided equally among team members.
Modify: The cash rewards may be replaced with point rewards or pennies. Using pennies lowers the total cash value to the class from about $50 to about $5.