By:  Neil E. Cotter

Statistics

 

 

Confidence Intervals

 

 

Activity (Loans)

 

 

teacher
 
 
 

 

Activity:  The making of loans depends on statistics describing the probability that customers will pay back loans.  In this activity, students are given data on how much loan customers paid back on several loan types. They process the data and decide which loans they will make.  Students start with $1.00.  They choose what loans to make with their money.

There are two rounds of loans.  In each round, there are two loan types to choose from.  Some data on payback rates for the loans is given.  Students get to decide how much of their $1 to invest in each type of loan.  Students work in groups.  Everyone in a group must invest the same amounts as the others.

Students may compute the sample mean,  where n is the number of customers, and the xi are the amounts paid back by each loan customer.

Students may also compute the sample standard deviation, .

Advanced students:

Having computed these values, students can compute a confidence interval.  They would use  where ta/2 is a critical value of the student distribution obtained from a table with a being the p-value such as 0.01 (meaning the probability of being so far out on the tails of the probability distribution is 0.01) and the degrees of freedom used for the table is n = n – 1.  A table for the student distribution is available on Wikipedia:

http://en.wikipedia.org/wiki/Student's_t-distribution  (table is near bottom of page)

Setting Up:

Groups of four students work well for this activity.  For the first round, one student can compute the sample mean, and another can compute the sample standard deviation.  With two loans, that makes four students.

 

Data for Students for Round 1:

Loan Type I Return (on loan of $1.00)

Customer

A

B

C

Paid Back

$1.60

$2.00

$1.20

Loan Type II Return (on loan of $1.00)

Customer

A

B

C

D

E

Paid Back

$1.65

$1.50

$1.35

$1.50

$1.35

 

For Teacher:

Data underlying Loan Type I:  Roll one 6-sided die.  Take number  times by $0.40.

Expected value is m = 1 • 3.5 • $0.40 $1.40.

Standard deviation is  =

Students may compute the sample mean,

Students may compute the sample standard deviation,  = $0.40

Advanced students:

Use critical value ta/2 for n = 3 (n = 2) and a = 0.1.

Confidence interval is


 

Data underlying Loan Type II:  Roll 3 dice, multiply sum by $0.15.

Expected value is m = 3 • 3.5 • $0.15 =  $1.58.

Standard deviation is  = .

Students may compute the sample mean,  = $1.17

Students may compute the sample standard deviation,  = $0.45

Advanced students:

Use critical value ta/2 for n = 5 (n = 4) and a = 0.1.

 or $0.99 to $1.57.

The data suggest that the second loan is a better bet, which is true.

Processing Loans for Round 1:

Have students write their names and the amount they are investing in Loan Type I and Loan Type II on a 3 x 5 index card.  They hand in the cards before the processing occurs.

For Loan Type I, roll 1 die and multiply by $0.40 to compute the payoff per dollar.  Multiply by the amount the students invested in Loan Type 1.  Subtract the amount the students invested in Loan Type I to find the increase or decrease in the group's funds.  See calculations sheet.

For Loan Type II, roll 3 dice and multiply sum by $0.15 to compute the payoff per dollar.  Multiply by the amount the students invested in Loan Type II.  Subtract the amount the students invested in Loan Type II to find the increase or decrease in the group's funds.  See calculations sheet.

Record the each group's new amount on their index card.

 

Data for Students for Round 2:

For Round 2 the data illustrates how much tighter a confidence interval becomes when more samples are available.  The students are given the sample mean and sample standard deviation directly.  (It would take too long to compute these quantities from n = 16 samples.)

Loan Type III Return (on loan of $1.00)

Customer

A

B

C

Paid Back

$0.40

$2.00

$1.60

n = 3 customers

 (average amount paid back on a $1.00 loan)

 (sample standard deviation of amount paid back on a $1.00 loan)

 

Loan Type IV Return (on loan of $1.00)

Customer

A

B

C

D

E

F

G

...

Paid Back

$1.40

$1.30

$1.70

$1.20

$2.20

$1.60

$1.80

...

n = 16 customers

 (average amount paid back on a $1.00 loan)

 

For Teacher:

Data underlying Loan Type III:  Roll 1 die and multiply by $0.40 = Loan Type I.

All calculations are the same as for Loan Type I.

Data underlying Type IV loan:  Roll 5 dice and multiply by $0.10.

Expected value is m = 5 • 3.5 • $0.10 = $1.75.

Standard deviation is  = .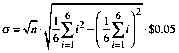

Advanced students:

Use critical value ta/2 for n = 16 (n = 15) and a = 0.1.

 

Loan IV has a better expected value and tighter variance, but students can make more from Loan III if they get lucky.

Processing Loans for Round 2:

Students may loan any or all of the amount they have after round 1.  They work in the same groups as before.  Have students write the amount they are investing in Loan Type III and Loan Type IV on their 3 x 5 card.  They hand in the cards before the processing occurs.

For Loan Type III, roll 1 die and multiply by $0.40 to compute the payoff per dollar.  Multiply by the amount the students invested in Loan Type III.  Subtract the amount the students invested in Loan Type III to find the increase or decrease in the group's funds.  See calculations sheet.

For Loan Type IV, roll 5 dice and take sum times $0.10 to compute the payoff per dollar.  Multiply by the amount the students invested in Loan Type IV.  Subtract the amount the students invested in Loan Type IV to find the increase or decrease in the group's funds.  See calculations sheet.

Payoff students with cash!