Nonlinear Systems/Differential Equations

Shifting Origin

 

 

 

Tool:      We may shift the origin and rewrite autonomous differential equations

               or        

                  in terms of perturbations, 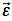, around a (constant) point, .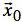

                  The derivatives of perturbations are the same as derivatives of state variables. In other words:

                    and             

                  Thus, we may rewrite the equations in terms of perturbations:

   

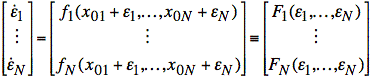
or

     

Note:      We may use the perturbation model at any point (not just fixed points).

Note:      The behavior of the system for small perturbations is the same as the linearized equations, (unless the real part of some eigenvalue equals zero—in which case it may or may not be the same). See stability for linearized equations.

Note:      We use the perturbation model to analyze stability around fixed points. The stability of the perturbation model is the same as the stability of the original system, unless some eigenvalues are zero.

Note:      In a linear matrix differential equation, the perturbation model allows us to eliminate the added constant vector when determining stability.